TRANSFORMATEURS D’ÉNERGIE ÉLECTRIQUE

TRANSFORMATEURS D’ÉNERGIE ÉLECTRIQUE

Les transformateurs sont des machines électriques statiques dont la fonction est d’élever ou d’abaisser la tension d’un circuit électrique parcouru par un courant alternatif sans en modifier la fréquence. Ils jouent un rôle essentiel dans le transport de l’énergie électrique à distance. En effet, les tensions de fonctionnement des machines génératrices n’excèdent pas une vingtaine de kilovolts en courant alternatif. Or le transport de grandes puissances sur des distances notables ne peut être réalisé de façon économique que s’il est effectué à très haute tension, soit plusieurs centaines de kilovolts. Il est donc nécessaire d’installer, à proximité immédiate des groupes générateurs, des transformateurs «élévateurs» de tension. On devra trouver des appareils «abaisseurs» aux points de fourniture de l’énergie électrique, les tensions normales d’utilisation étant comprises entre quelques centaines et quelques milliers de volts.

Il existe d’autres types de transformateurs employés principalement pour des mesures de grandeurs électriques. Leur principe de fonctionnement est tout à fait identique à celui des transformateurs de puissance, mais leurs caractéristiques peuvent avoir des ordres de grandeur tout à fait différents.

L’ancêtre du transformateur est le «générateur secondaire» imaginé par l’Anglais J. D. Gibbs et le Français L. Gaulard et construit à Londres en 1883. La première transmission électrique en courant alternatif utilisant des machines de ce type est réalisée par Gaulard en 1884 entre l’exposition de Turin et la gare de Lanzo distante de trente-sept kilomètres. Trois ingénieurs hongrois, M. Deri, O. Blathy et K. Zipernowsky, qui assistent à cette exposition, remarquent les graves imperfections du générateur secondaire, notamment son circuit magnétique ouvert. Ils conçoivent en 1885 le transformateur sous une forme qu’il a pratiquement conservée de nos jours.

Principe de la bobine à noyau de fer

Soit une carcasse magnétique en forme de tore supportant un enroulement de n spires alimenté par une source de tension sinusoïdale de valeur instantanée v et de période T. Soit en valeurs instantanées: i le courant traversant l’enroulement de résistance R; h et b l’excitation et l’induction magnétique; S, a et V la section droite, la longueur de la ligne moyenne et le volume du tore.

Le matériau de perméabilité magnétique 猪 est caractérisé ^{[cf. MAGNÉTISME]} par un cycle d’hystérésis b (h ) de surface 遼 (fig. 1 a). On suppose, dans un premier temps, 猪 infini. Les lignes de forces du champ magnétique sont en conséquence canalisées par le tore (hypothèse de l’absence de fuites magnétiques).

La tension instantanée aux bornes de l’enroulement s’exprime par:

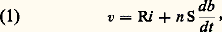tandis que le théorème d’Ampère ^{[cf. ÉLECTRO-AIMANTS]} conduit à:

On peut déduire des relations (1) et (2) l’équation (3) qui traduit le bilan énergétique durant une période T:

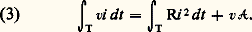Il apparaît que l’énergie fournie par la source se divise en un terme correspondant à l’effet Joule au niveau de l’enroulement, et en un terme v 遼 résultant du phénomène d’hystérésis. Ce dernier se traduit par une libération d’énergie thermique dans le matériau magnétique.

Par ailleurs, à partir des graphes b (h ) et v(t ), où t désigne le temps, en tenant compte de la relation (2) et en négligeant R, on peut déterminer (fig. 1 b) le graphe i (t ). Le courant i est périodique mais non sinusoïdal. Cela rend impossible l’utilisation des méthodes habituelles de l’électrotechnique (représentation complexe, diagramme vectoriel...). Aussi substitue-t-on au courant réel un courant «sinusoïdal équivalent» provoquant les mêmes effets énergétiques que le précédent, c’est-à-dire les mêmes pertes par effet Joule et les mêmes dissipations par hystérésis. Ces conditions, qui se traduisent par des pertes réelles par effet Joule, RI², et des dissipations énergétiques réelles, VI cos 﨏, sont suffisantes pour déterminer le module I de ce courant et son déphasage 﨏 sur V (les valeurs surlignées sont des quantités complexes).

En définissant «l’angle d’avance hystérétique» 見^H = ( 神/2) 漣 﨏, on peut alors poser:

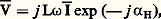ce qui revient à représenter la bobine à noyau de fer par l’admittance complexe ^{[cf. CIRCUITS ÉLECTRIQUES]}:

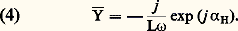Si les conditions de saturation du circuit magnétique sont telles qu’on ne peut considérer 猪 comme infini, il faut tenir compte de la fraction des lignes de forces du champ magnétique qui se referment dans l’air. Une façon commode de traiter ce problème est d’introduire une inductance de fuite l . Cet acte est légitime parce que la réluctance du circuit magnétique «fer-air» dépend essentiellement du trajet des lignes de forces dans l’air de perméabilité constante. Dans ces conditions, l’équation (1) devient:

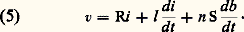La figure 2 résume l’ensemble des résultats fournis par les équations (4) et (5). Il y apparaît la résistance R, l’inductance de fuite l , la conductance et la réactance constituant l’admittance Y 漣.

La bobine réelle est ainsi représentée par un modèle physique de telle façon que les fonctionnements respectifs de ces deux systèmes sont identiques dans le cadre des approximations faites. Il peut être tenu compte des pertes par courants de Foucault au sein du matériau magnétique en adaptant convenablement l’admittance Y 漣. L’ensemble des dissipations énergétiques par hystérésis et courants de Foucault est alors désigné sous le terme de pertes électromagnétiques . Ces considérations fournissent les éléments de base de la théorie du transformateur.

Le transformateur monophasé

Le transformateur monophasé (fig. 3) est essentiellement constitué d’un circuit magnétique en tôles de fer muni de deux bobines B¹ et B² comportant respectivement n ¹ et n ² spires. La bobine B¹ alimentée par une source de tension alternative S^a est traversée par un courant alternatif i ¹ qui crée dans le circuit magnétique un flux variable. Celui-ci engendre dans la bobine B² une force électromotrice (f.é.m.) induite dont la fréquence est celle de la source S^a , et qui peut être utilisée pour alimenter un récepteur d’impédance Z. Ainsi, par induction mutuelle, une fraction de la puissance alternative fournie par la source S^a au circuit B¹ (primaire ) est transférée au circuit constitué de Z et de B² (secondaire ).

Théoriquement, rien ne s’oppose à ce que chaque bobine, B¹ ou B², joue indifféremment le rôle de primaire ou de secondaire. Pratiquement, des problèmes d’isolement et de sécurité conduisent souvent à imposer à chacun de ces deux circuits un rôle défini.

Soit, en notations complexes, V¹ la tension appliquée aux bornes de B¹ (la valeur instantanée étant v¹ = V¹ 連2 cos 諸t ); V² la tension recueillie aux bornes de B²; R¹ et R² les résistances respectives des deux enroulements; 淋 漣¹ et 淋 漣² les flux dans ces deux enroulements; m = (n ²/n ¹) le «rapport de transformation» (par définition).

Les conventions de signes étant précisées sur la figure 4, le flux variable 淋 漣¹ induit dans le primaire une f.é.m. égale à 漣 jn ¹ 諸淋 漣¹. L’application de la loi d’Ohm aux bornes de cet élément conduit à:

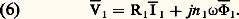De même 淋 漣² induit dans le secondaire une f.é.m. égale à 漣 jn ² 諸淋 漣², et les équations électriques relatives à ce circuit s’écrivent:

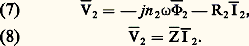Le problème qui se pose généralement est le suivant: on se donne un régime secondaire V², I 漣² (soit V², I² et le déphasage 﨏² de I 漣² sur V²), c’est-à-dire un état de charge du transformateur. Quel est le régime primaire V¹, I 漣¹ (V¹, I¹, 﨏¹) correspondant?

Ce problème est résolu de façon plus ou moins précise selon la nature des approximations que l’on introduit.

Transformateur parfait

L’approximation la plus grossière est l’approximation dite du transformateur parfait. Un transformateur parfait satisfait aux conditions suivantes:

– les fuites magnétiques sont nulles, c’est-à-dire que le même flux parcourt les deux enroulements B¹ et B²; on a donc 淋¹ = 淋² = 淋;

– les résistances R¹ et R² des enroulements sont négligeables; on a donc R¹ = R² = 0;

– la perméabilité 猪 du circuit magnétique est infinie; il en résulte que la réluctance 倫 du circuit magnétique (qui est égale au rapport a/ 猪S) et les pertes électromagnétiques sont nulles.

Dans ces conditions, les équations (6) et (7) deviennent:

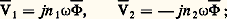elles conduisent à:

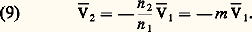D’autre part, la loi d’Hopkinson s’écrit, dans le cadre des hypothèses faites,

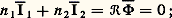on en déduit:

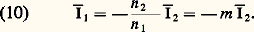La puissance primaire P¹ = V¹I 漣¹ est intégralement transférée au secondaire. Le modèle du transformateur parfait et les équations (9) et (10) qui en découlent constituent une approximation valable dans le cas de transformateurs de faible puissance, utilisés par exemple dans les montages électroniques.

Transformateur réel

Dans le cas de machines plus importantes, il devient nécessaire de tenir compte:

– des fuites magnétiques; on introduit à cet effet les inductances de fuites partielles primaire et secondaire, l ¹ et l ², et l’on admet que les flux 淋 漣¹ et 淋 漣² se décomposent en un flux commun 淋 漣 et des flux de fuite l ¹(d I 漣¹/dt ) et l ²(d I 漣²/dt ) relatifs respectivement au primaire et au secondaire; cette décomposition est arbitraire et ne se justifie que par les simplifications qu’elle introduit;

– des résistances respectives R¹ et R² des bobines B¹ et B²;

– des pertes électromagnétiques.

Les équations générales (6) et (7) deviennent alors:

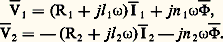D’où, en éliminant 淋 漣,

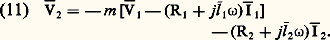À partir de la théorie du transformateur parfait, la relation (11) conduit au schéma de la figure 4 a. Pour tenir compte des pertes électromagnétiques, il reste à introduire, conformément à la théorie de la bobine à noyau de fer, une admittance Y 漣. La figure 4 b qui en résulte représente le schéma électrique équivalent définitif du transformateur réel.

On peut inclure à ce niveau une approximation appelée hypothèse de Kapp , qui se traduit par la relation:

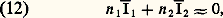expression rigoureuse seulement dans le cas du transformateur parfait.

Compte tenu de (12), l’équation (11) devient alors:

sachant que:

La relation (13) est appelée équation de Kapp. Le diagramme de Kapp qui la traduit est tracé sur la figure 5. Ce diagramme, obtenu en partant du régime secondaire V², I 漣², 﨏², permet de déterminer le régime primaire V¹, I 漣¹, 﨏¹, le rendement 兀 = V²I 漣²/V¹I 漣¹ et la chute de tension en charge 﨎 = m V¹ 漣 V². L’utilisation de ce diagramme est rendue délicate parce que le triangle ABC est en réalité beaucoup plus petit qu’il n’apparaît sur la figure.

Le transformateur triphasé

Trois transformateurs monophasés identiques, du type «à colonne», c’est-à-dire dont les enroulements sont portés par un même noyau du circuit magnétique, peuvent être réunis en une machine unique présentant la symétrie de révolution. L’axe du système est formé par les noyaux libres; les transformateurs sont disposés régulièrement en étoile autour de cet axe. Les enroulements primaire d’une part, secondaire de l’autre sont groupés de façon à constituer deux bobinages triphasés et alimentés par des systèmes de tensions triphasées.

En marche normale, les réseaux sont équilibrés. Il en résulte que la somme des flux dans une section du noyau central est nulle et que ce dernier perd son rôle de conducteur magnétique. Aussi substitue-t-on à la disposition théorique qui vient d’être décrite la disposition plus simple de la figure 6. Le noyau central est supprimé et les axes des noyaux qui supportent les bobinages sont dans un même plan.

La théorie du transformateur monophasé s’applique à chaque phase. Toutes les grandeurs étant relatives à une phase, la relation de Kapp s’écrit: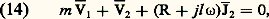

où, selon les conventions habituelles, V désigne une tension simple et J 漣 un courant de phase.

La figure 7 représente un transformateur triphasé couplé en étoile au primaire et au secondaire. Dans ce cas, les quantités V et J 漣 sont respectivement reliées aux tensions entre phases (tensions composées) U 漣 et aux courants de ligne I 漣 par les relations:

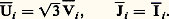Technologie des transformateurs

Le circuit magnétique d’un transformateur est constitué par des tôles d’acier au silicium de 35 à 40/100 mm d’épaisseur, isolées entre elles et fortement comprimées par des boulons et des plaques de serrage. L’acier au silicium présente en effet un cycle d’hystérésis étroit, une résistivité élevée qui limite les courants de Foucault et une grande stabilité. Dans les machines de puissance, les matériaux magnétiques à «cristaux orientés» présentent une anisotropie qui concourt encore à la diminution des pertes électromagnétiques. La section des noyaux est en croix de Saint-André, ce qui favorise le refroidissement.

Les enroulements sont en fils ou en barres de cuivre ou d’aluminium, émaillés ou enrubannés de coton, de papier ou de toile vernie. Les enroulements divisés en «galettes» sont exécutés sur des formes circulaires et ensuite imprégnés de vernis. Ils sont comprimés lors du montage sur les noyaux. Cette opération est destinée à stabiliser le vernis et à permettre au bobinage de résister aux efforts électromagnétiques.

Les enroulements sont isolés du circuit magnétique et du milieu extérieur ou de l’enveloppe métallique de la machine (cuve) par des diélectriques gazeux (air, hexafluorure de soufre), liquides (huile minérale, hydrocarbure chloré, tel le Pyralène) ou solides (quartz). Le refroidissement est assuré, dans le cas des transformateurs à l’air libre, par circulation naturelle de l’air ambiant et, dans celui des transformateurs immergés, à l’aide de radiateurs et d’échangeurs de chaleur.

Enfin, le raccordement entre les extrémités des enroulements et les réseaux s’effectue, le cas échéant, à travers la cuve du transformateur, à l’aide d’une «traversée», tige conductrice entourée d’un manchon isolant, huile ou porcelaine.

Encyclopédie Universelle. 2012.